Archives
br Results and discussion br Conclusion br Experimental
Results and discussion
Conclusion
Experimental section
Pharmacological studies
Introduction
Survival analysis is a set of statistical methods that aim at modeling the relationship between a set of predictor variables and an outcome variable and, in particular, prediction of the time when an event occurs [1]. In medical sciences, survival analysis is primarily used to predict events such as death, relapse, or development of a new disease. One of the most popular methods used in survival analysis is called the Cox\'s proportional hazards (CPH) model [2]. The CPH model is similar to a multiple linear regression technique that explores the relationship between a hazard and related independent explanatory variables over a period of time. It describes the impact of a risk factor on a treatment of patients through a parameter called hazard ratio [3]. Hazard ratio between two groups, e.g., treatment and control group in a clinical trial, represents the relative likelihood of survival at any time in the study and is usually assumed to be constant over time.
The CPH model has been widely used for predicting patient survival rate. For example, the Seattle Heart Failure Model [4] uses the CPH model to predict 1-, 2-, and 3-year survival of ACSF failure patients. The Registry to Evaluate Early and Long-Term Pulmonary Arterial Hypertension (PAH) Disease Management (REVEAL) [5] also uses the CPH model to derive the Risk Score Calculator to determine probability of a PAH patient survival within an enrolled year.
This paper focuses on an alternative tool for survival analysis: Bayesian networks. Compared to the CPH model, a Bayesian network can model explicitly the structure of the relationships among explanatory variables [6]. Researchers can intuitively design and build a Bayesian network from expert knowledge or available data. The network can depict a complex structure of a problem and provide a way to infer probability distributions that are suitable for prognosis and diagnosis, for example in medical decision support systems [7]. However, building Bayesian networks based purely on expert knowledge can be a time-consuming and costly task. Luckily, many CPH models can be found in the literature. They are typically published as a set of numerical coefficients along with their significance levels. No original data are usually available. To use the knowledge encoded in these CPH models, an interpretation of the CPH parameters is needed. We propose such a Bayesian network interpretation of the CPH model (BN-Cox), discuss its advantages and potential challenges, including those related to its representational and computational complexity.
Cox\'s proportional hazard model
The probability of an individual surviving beyond a given time t, i.e., the survivor function, is defined as T is a variable denoting the time of occurrence of an event of interest. The survival probability at the beginning, i.e., at time , may be 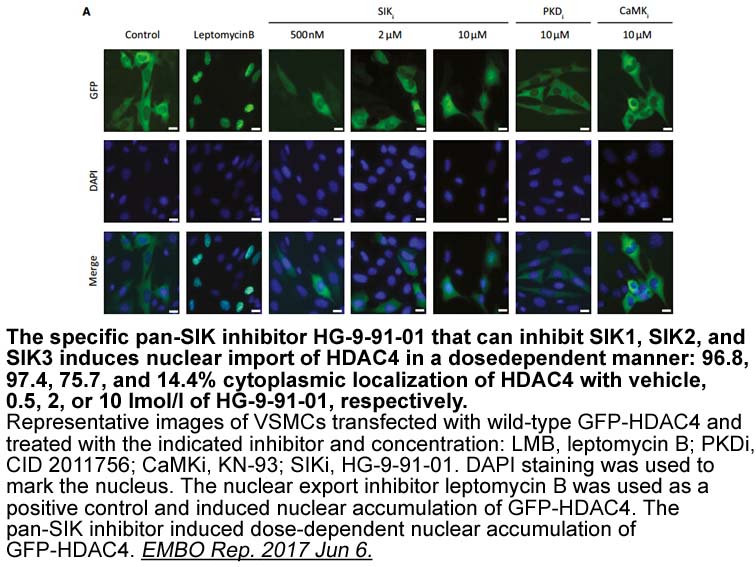 equal to 1 or to some baseline survival probability, which will drop down to zero over time. While the survivor function represents the probability of survival, the hazard function, given by where T is also a time variable, represents the risk of event occurrence at time t. The hazard is a measure of risk at a small time interval △t and is sometimes called a hazard rate, expressing the number of events per interval of time [1].
The relationship between the hazard function and the survivor function (see more details in Allison\'s textbook [1]) is described as or as Hence, we can estimate the survival probability from the hazard function. In survival analysis, the hazard function can be represented by any probability distribution (e.g., exponential distribution) or can be modeled by regression techniques. One of the most popular survival analysis techniques is the Cox\'s proportional hazard (CPH) model [2]. The CPH model provides assessment of survival based on risk factors associated with the events indicated in the model. The simplest CPH model consists of time-independent risk factors. The hazard function in such a CPH model is expressed as This hazard model is composed of two main parts: the baseline hazard function, , and the set of effect parameters, . The baseline hazard function determines the risks at an underlying level of explanatory variables, i.e., when all risk factors are absent. According to Cox [2], Saturation density can be unspecified or follow any distribution, which makes the CPH model semi-parametric. The βs are coefficients corresponding to the risk factors, .
equal to 1 or to some baseline survival probability, which will drop down to zero over time. While the survivor function represents the probability of survival, the hazard function, given by where T is also a time variable, represents the risk of event occurrence at time t. The hazard is a measure of risk at a small time interval △t and is sometimes called a hazard rate, expressing the number of events per interval of time [1].
The relationship between the hazard function and the survivor function (see more details in Allison\'s textbook [1]) is described as or as Hence, we can estimate the survival probability from the hazard function. In survival analysis, the hazard function can be represented by any probability distribution (e.g., exponential distribution) or can be modeled by regression techniques. One of the most popular survival analysis techniques is the Cox\'s proportional hazard (CPH) model [2]. The CPH model provides assessment of survival based on risk factors associated with the events indicated in the model. The simplest CPH model consists of time-independent risk factors. The hazard function in such a CPH model is expressed as This hazard model is composed of two main parts: the baseline hazard function, , and the set of effect parameters, . The baseline hazard function determines the risks at an underlying level of explanatory variables, i.e., when all risk factors are absent. According to Cox [2], Saturation density can be unspecified or follow any distribution, which makes the CPH model semi-parametric. The βs are coefficients corresponding to the risk factors, .